美国加州大学伯克利分校哲学系教授韦斯利·霍利迪“非经典逻辑的奇遇”系列讲座第一讲顺利举行
点击次数: 更新时间:2023-05-23
本网讯(通讯员唐瑞雪)5月20日上午,应我院陈波教授邀请,美国加州大学伯克利分校哲学系教授韦斯利·霍利迪(Welsley Holliday)做了“非经典逻辑的奇遇”(Adventures in Non-classic Logics)系列讲座的第一讲。讲座由陈波教授主持,我院博士后樊达评议,来自国内外的400余名观众参加了此次线上讲座。
本次讲座主要阐述了经典逻辑在数学和科学、自然语言、自然推理这三方面遭遇的挑战,而这些挑战促进了非经典逻辑的发展。

首先,霍利迪讨论了经典逻辑在数学和科学领域面临的挑战。在数学领域,他以圆周率π为例来说明数学中的“非构造性证明”(nonconstructive proof)。运用归谬原则论证在π的十进制展开形式中,1到9中的某个数字会无限次出现。但这个证明并没有告诉我们究竟哪个数字会无限次出现。这样的证明被称为非构造性证明,其特征是虽然证明了存在着某物具有特定的性质,但是我们还没有构造出一个例子并证明它具有这种性质。非构造性证明遭到直觉主义逻辑拥护者的拒斥。他们认为,如果可以证明 ![]() ,就可以证明对某个项 t
,就可以证明对某个项 t ![]() 。进而,他们也拒斥在非构造性证明中所使用的归谬原则。其次,关于数学的非实在论对经典逻辑中的排中律提出了挑战。例如,费弗曼(S.Feferman)认为数学中的基本对象只以思想概念的形式存在,因此对集合进行无穷量化的集合论中的某些陈述
。进而,他们也拒斥在非构造性证明中所使用的归谬原则。其次,关于数学的非实在论对经典逻辑中的排中律提出了挑战。例如,费弗曼(S.Feferman)认为数学中的基本对象只以思想概念的形式存在,因此对集合进行无穷量化的集合论中的某些陈述 ![]() ,费尔曼拒斥
,费尔曼拒斥 ![]() 。
。
在科学领域,霍利迪以量子力学为例,以实验的形式表明在经典逻辑的经典性(classicality)、启示性(revelation)、独立性之间存在冲突。经典性是指对于经典逻辑中的定理 ![]() ,
, ![]() (P(
(P( ![]() ) 指
) 指 ![]() 的发生概率);如果
的发生概率);如果 ![]() 在经典逻辑中不相容,那么
在经典逻辑中不相容,那么 ![]() 。启示性是指如果对于命题A,
。启示性是指如果对于命题A, ![]() 并且
并且 ![]() ,但是
,但是 ![]() 也是如此。独立性是指由A、B等产生的命题概率独立于测量设置的选择。面对上述三个原则之间的冲突,有一种方案是放弃经典性原则,即拒斥经典逻辑中的分配原则,即
也是如此。独立性是指由A、B等产生的命题概率独立于测量设置的选择。面对上述三个原则之间的冲突,有一种方案是放弃经典性原则,即拒斥经典逻辑中的分配原则,即 ![]() 和
和 ![]() 。
。
其次,霍利迪分析了自然语言对经典逻辑提出的挑战。一方面,经典逻辑的中的否定和分配律不适用于包含认知模态的语句。霍利迪以维特根斯坦语句为例来说明经典逻辑中对于否定的认识不能用来分析包含模态词的语句。维特根斯坦语句具有以下四种形式:p∧◇¬p、¬p∧◇p、◇p∧¬p、◇¬p∧p。从直觉上来看,维特根斯坦语句包含着矛盾,即p∧◇¬p├⟂,如“玛丽生病了并且她可能没有生病”。而在经典逻辑中,否定具有伪互补性(pseudocomplementation),即 ![]() ,那么
,那么 ![]() 。这样看来,由p∧◇¬p├⟂,可推出◇¬p├¬p。但是这个结果明显违反常识。此外,经典逻辑中的分配律也无法用于分析包含认知模态的语句。如从“约翰可能有罪并且他可能无罪,并且他是无罪的或者他是有罪的”,运用经典逻辑的分配律可以推出“约翰有罪并且他可能无罪,或者他无罪并且可能有罪”。从为真的前提运用经典逻辑的分配律得到了为假的结论。另外一方面,自然语言也无法有效地处理模糊性问题。霍利迪以颜色悖论为例指出,模糊性问题对经典逻辑的二值原则构成了严重的挑战,因为我们很难确定包含模糊谓词的语句为真还是为假。为了解释模糊性问题,直觉主义逻辑拒斥排中律。
。这样看来,由p∧◇¬p├⟂,可推出◇¬p├¬p。但是这个结果明显违反常识。此外,经典逻辑中的分配律也无法用于分析包含认知模态的语句。如从“约翰可能有罪并且他可能无罪,并且他是无罪的或者他是有罪的”,运用经典逻辑的分配律可以推出“约翰有罪并且他可能无罪,或者他无罪并且可能有罪”。从为真的前提运用经典逻辑的分配律得到了为假的结论。另外一方面,自然语言也无法有效地处理模糊性问题。霍利迪以颜色悖论为例指出,模糊性问题对经典逻辑的二值原则构成了严重的挑战,因为我们很难确定包含模糊谓词的语句为真还是为假。为了解释模糊性问题,直觉主义逻辑拒斥排中律。
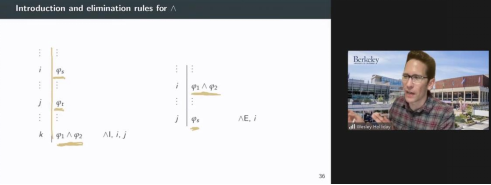
最后,霍利迪指出经典逻辑在数学、科学和自然语言遭遇地挑战相应地威胁到自然推理中所运用的归谬原则和重述原则(Reiteration)。归谬原则在上面已经谈到,这里主要阐述重述原则。如果承认重述原则,那么可以从◇p合乎逻辑地推出p。但是这个结论是违反常识的。
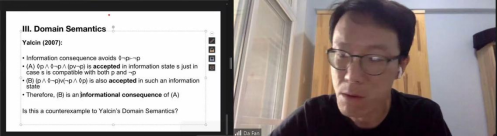
在评议环节,樊达围绕着“如何理解‘即使在证明中已经有◇p,但在子证明中也不能使用重述原则得到◇p’” 、“如何理解在包含模态词的自然推理中使用的否定后件原则(MT)”、“领域语义学(Domain Semantics)中对◇¬p├¬p的解释”等问题进行提问。霍利迪回应称,自己会在下次讲座中详细地阐述重述原则,解释为什么即使在证明中已经确定有◇p,但在接下来的子证明不能使用重述原则。对于否定后件原则,霍利迪认为对于包含模态词的语句,存在着前提为真而结论为假的反例。
陈波教授就“如何看待威廉姆森对模糊性问题的解决方案”、程勇教授就“是否在物理学中存在着特定形式的逻辑学”和“仅使用直觉主义逻辑是否会损害部分现有的科学知识”分别进行提问。霍利迪分别进行了简单回应,自己认为威廉姆森“在秃头与非秃头之间存在明确的界限,只是我们现在还不知道”的观点有趣,对我们如何可以知道这个界限表示怀疑。
(编辑:邓莉萍 审稿:刘慧)
